MATEMÁTICA

  Miércoles 28 de octubre.

¡¡¡¡Buenas tardes 7mo grado!!!! ¿Cómo están geni@s? aquí estamos nuevamente. ¡¡¡Linda semana para tod@s!!!!

Esta semana trabajaremos:

7º "A y B": miércoles y jueves actividades publicadas en el blog y el viernes corrección grupal-puesta en común por zoom a las 11:30 hs.  

Actividad de hoy para ambos séptimos...

Continuaremos trabajando con polígonos (figura de n lados). La semana pasada trabajamos y deducimos que la cantidad de diagonales por vértice de un polígono es igual a n - 3, que la cantidad de triángulos que lo conforman es igual a n - 2, que la suma de los ángulos interiores es igual a 180º · (n - 2). También deducimos que la fórmula para calcular el área de un polígono regular es igual a  P · ap/2. Hoy conoceremos y trabajaremos con el ángulo central de un polígono regular.

Trabajaremos en las actividades 1; 2 y 3 que se encuentran al final de la publicación.

Actividad 1. nos piden averiguar la medida del ángulo central señalado en el octógono regular y calcular cuánto mide cada uno de sus ángulos interiores. Como sabemos, el octógono regular está conformado por ocho triángulos isósceles iguales. Sabiendo que la suma de los ocho ángulos centrales miden 360º, fácilmente podremos deducir la medida de cada ángulo central, cierto? Finalmente, nos piden calcular la medida de cada ángulo interior del octógono regular. ¿Qué relación podemos establecer entre la medida del ángulo central y el ángulo interior de un polígono regular? 

Ejercicio 2. aquí tenemos que decidir si es posible construir polígonos regulares colocando varios triángulos iguales, por ejemplo, los del ítem a), uno al lado del otro, intentando conformar y "cerrar" un polígono regular de cierta cantidad de lados y que cada lado del polígono regular mida 3 cm. ¿Con cuáles de los triángulos a); b) o c) es posible o no, construir polígonos regulares? De poder construirlos, de qué polígonos regulares se trata? 

Ejercicio 3. aquí nos piden completar el cuadro. Hay un error, 45º corresponde a la medida del ángulo central y NO a la medida del ángulo interior, está en la casilla equivocada, así que hay que cambiar la medida (45º) a la casilla de la izquierda.... ¿Se animan a completarlo? 

¡¡¡Vamos con estos nuevos desafíos!!!!

ESTA TAREA NO SE ENTREGA, la corregiremos el viernes por zoom a las 11:30 hs. L@s espero a tod@s!

Todas las dudas y entregas de Matemática las realizamos al correo:

matematica7andresferreyra@gmail.com

Pregunten todas sus inquietudes, respetando días y horarios de clase...

Recuerden, aquí estoy para ayudarl@s.

Nos seguimos leyendo mañana. 

Abrazote virtual!!! L@s extraño y l@s quiero muchooooo!!!

Profe Silvia Giuli.

En la carpeta

7º "A y B"

28/10 

Polígonos regulares: ángulo central

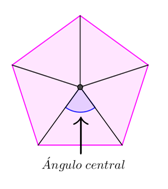
• Se llama ángulo central de un polígono regular al que queda delimitado por dos segmentos: uno tiene un extremo en el centro del polígono y el otro extremo en cualquier vértice. El otro segmento también tiene un extremo en el centro del polígono y el otro en un vértice consecutivo al vértice anterior.
• La suma de todos los ángulos centrales de un polígono es 360º.

 Trabajamos en los ejercicios 1; 2 y 3 de la siguiente actividad: